The Birthday Paradox
Consider the question, how many people must be a room such that the probability of at least two will share a birthday exceeds 50%?
You might guess about 182 because it’s about half the days in a year, or 100 because it’s a nice round number. However, the answer might surprise you.
The correct answer is just 23 people. How can this be true?! The answer lies in probability theory. Let the event A be that of a group of k people not having any repeated birthdays, and let B be that of a group of k people having at least two who share a birthday, i.e. \(P(B) = 1 - P(A)\).
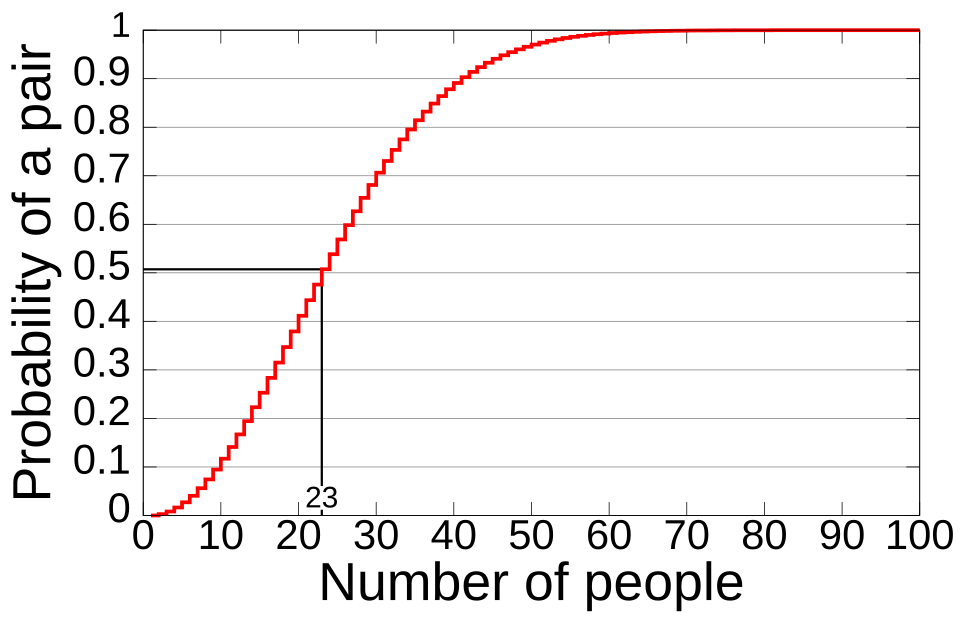
To calculate the number of k persons to exceed 50% one technique we might use is to decrement the number of possible shared birthdays for \(n+1\) people. For person 1 there is 100% chance they don’t share their birthday with another person, when adding person 2, there is a \(\frac{364}{365}\) chance they don’t share their birthday with person 1, and this continues as a conditional probability until you reach >50%.
\[P(A)= \frac{365}{365} \times \frac{364}{365} \times \cdots \times \frac{343}{365} \approx 0.493\] \[\therefore P(B) \approx 1 - 0.493 = 0.507\]A more concise way of representing this is the probability function \(\bar{p} = \frac{365!}{365^n(365-n)!}\). An approximation to try (that doesn’t require numerical methods) is \(n\geq \frac{1}{2} + \sqrt{\frac{1}{4} + 2\times\ln{2}\times 365}\).
I hope you liked this introduction to probability with the Birthday Paradox. Stay curious!